Over the last two days I have been working on some code to generate planets in MonoGame, the content of this post however is general enough to be transferred to any language you wish to use.
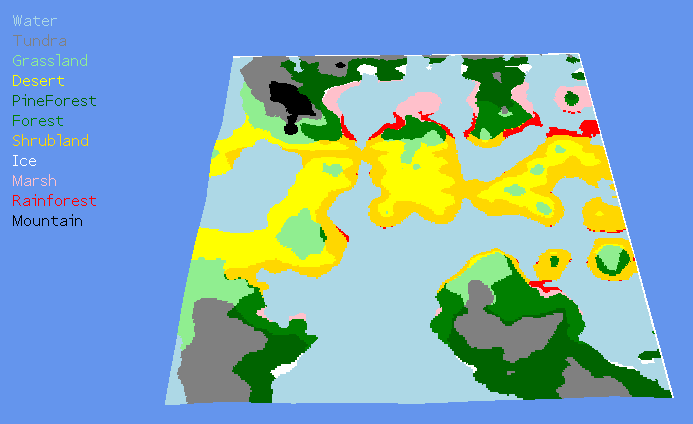
When I first started investigating planet generation I hoped to be able to transfer the code I developed for my square grid heightmap terrain (for which a biome map is pictured below) onto a sphere. The problem with this however is that you can’t wrap a square grid around a sphere without some distortion as you go towards the poles.
Such distortion could be avoided if you want to wrap a texture around a sphere by stretching the image as you go towards the poles of the planet. If this is what you want to do, then check out this page. As shown here, you could also use this to apply perlin noise to a planet.
After some more digging however I found a method for making spheres which is much more suited to what I wanted – icosahedron subdivision.
The icosahedron is the regular 3D solid with 20 faces, all of which are equilateral triangles. These shapes have several interesting properties, including that in the edge length 1 icosahedron the vertices lie on the corners of three golden rectangles.
The vertices of an edge length 1 icosahedron lie on the corners of three golden rectangles.
The important thing for us about this shape however is that each of these faces can be subdivided into four smaller equilateral triangles, and with some jiggery-pokery, we can push these out to the edges of a sphere. And because we subdivided the faces into more equilateral triangles, these too can be subdivided, and so on and so forth, in an iterative process that gets us ever closer to a sphere.

An icosahedron and its first two subdivisions. Source: RJ Mathar (http://www.mpia-hd.mpg.de/~mathar/) via Wikipedia.
A point on a surface of a sphere lies so that x2 + y2 + z2 = r2 so using this knowledge we can take the points on our icosahedron, and push them out to the surface of the sphere, allowing us to keep our subdivided shape spherical, opposed to a icosahedron but with a lot of triangles making up its faces.
Some really nice C# code for this generation process can be found over at Andreas Kahler’s blog, here.
My goal is to generate a planet, rather than a smooth sphere, and so here icosahedron subdivision has an important advantage over using distorted squares, and that is it can be used to generate fractal terrain as you subdivide, rather like how the diamond square or similar algorithms work for square grid based terrain – there will be more on this in my next post.